Pythonによる制御工学入門 第3回
前回と同様に、参考書の5章「閉ループ系に注目した制御設計」の
5.2「PID制御」のボード線図を自作の数値シミュレーションで再現する
前回は、制御対象の"生"のモデルの周波数特性を取得したが、
今回は、PID制御でフィードバック制御が働いている状態の周波数特性を取得する
P制御
垂直駆動アームのモデルに対して、制御を行っていく
import matplotlib.pyplot as plt import numpy as np import pandas as pd import control.matlab as pyctrl g = 9.81 # 重力加速度[m/s^2] l = 0.2 # アームの長さ[m] M = 0.5 # アームの質量[kg] mu = 1.5e-2 # 粘性摩擦係数[kg*m^2/s] J = 1.0e-2 # 慣性モーメント[kg*m^2] target = 30 # 目標角度 [deg] kp = 2.0
ステップ応答
下記のスクリプトで数値シミュレーションを行う
dt = 0.0001 t_s = [0.0] x_s = [0.0] v_s = [0.0] a_s = [0.0] F_s = [0.0] ref_s = [0.0] for i in range(20000): ref = target ref_s += [ref] F_s += [(ref - x_s[-1]) * kp] a_s += [(- mu * v_s[-1] - M * g * l * x_s[-1] + F_s[-1]) / J] v_s += [v_s[-1] + a_s[-1] * dt] x_s += [x_s[-1] + v_s[-1] * dt] t_s += [t_s[-1] + dt] df = pd.DataFrame() df['in'] = F_s[::100] df['out'] = x_s[::100] df.index = t_s[::100]
結果をプロットし、controlモジュールの結果と比較する
fig = plt.figure(figsize=(6, 5)) ax1 = fig.add_subplot(1, 1, 1) ax1.plot(df.index, df['out'], '.-', label='sim') # controlモジュールによるステップ応答と比較 P = pyctrl.tf([0, 1], [J, mu, M *g *l]) K = pyctrl.tf([0, kp], [0, 1]) Gyr = pyctrl.feedback(P * K, 1) y,t = pyctrl.step(Gyr, np.arange(0, 2, 0.01)) ax1.plot(t, y*target, '-', label='pyctrl') ax1.axhline(target, color="k", linewidth=0.5) ax1.set_xlim(0, 2); ax1.set_ylim(0, 50) ax1.legend(); ax1.grid() ax1.set_ylabel('y'); ax1.set_xlabel('t') fig.tight_layout()

周波数特性
0.01Hz ~ 10Hz までを等比で100分割する
hz_s = [] hz = 0.01 while True: if hz > 10 * 10 ** (3 / 100): break hz_s.append(hz) hz = hz * 10 ** (3 / 100)
各周波数の正弦波を目標に入れて周波数特性を取得する
dt = 0.0001 df_list = [] for hz in hz_s: t_s = [0.0] x_s = [0.0] v_s = [0.0] a_s = [0.0] F_s = [0.0] ref_s = [0.0] for i in range(50000): ref = target * np.sin(2.0 * np.pi * hz * t_s[-1]) ref_s += [ref] F_s += [(ref - x_s[-1]) * kp] a_s += [(- mu * v_s[-1] - M * g * l * x_s[-1] + F_s[-1]) / J] v_s += [v_s[-1] + a_s[-1] * dt] x_s += [x_s[-1] + v_s[-1] * dt] t_s += [t_s[-1] + dt] df = pd.DataFrame() df['in'] = ref_s[30000:] df['out'] = x_s[30000:] df.index = t_s[30000:] df_list += [df]
時系列波形からゲインと位相変化を取得する関数
from scipy.optimize import curve_fit def sin_func(x, p0, p1, p2): return p0 * np.sin(2.0 * np.pi * p1 * x + p2) def _convert_phase(phase): phase += 180 phase %= 360 if phase < 0: phase += 180 else: phase -= 180 return phase def _convert_param(param): param = param.copy() param[2] = param[2] / np.pi * 180 if param[0] < 0: param[0] = -param[0] param[2] += 180 param[2] = _convert_phase(param[2]) return param def calc_f_func(param1, param2): param1 = _convert_param(param1) param2 = _convert_param(param2) freq = param1[1] gain = param2[0] / param1[0] phase = param2[2] - param1[2] phase = _convert_phase(phase) return param1, param2, freq, gain, phase
周波数解析を実施
data_s = [] for hz, df in zip(hz_s, df_list): p0 = [target, hz, 0.0] p1, conv = curve_fit(sin_func, np.array(df.index), np.array(df['in']), p0=p0) p0 = [target, hz, 0.0] p2, conv = curve_fit(sin_func, np.array(df.index), np.array(df['out']), p0=p0) param1, param2, freq, gain, phase = calc_f_func(p1, p2) data_s.append([freq, gain, phase]) df_res = pd.DataFrame(data_s) df_res.columns = ['freq', 'gain', 'phase']
結果を表示する
これもcontrolモジュールと比較する
fig = plt.figure(figsize=(6, 5)) ax1 = fig.add_subplot(2, 1, 1) ax2 = fig.add_subplot(2, 1, 2) ax1.plot(df_res['freq'], np.log10(df_res['gain'])*20.0, 'o-', label='sim') ax2.plot(df_res['freq'], df_res['phase'], 'o-', label='sim') K = pyctrl.tf([0, kp], [0, 1]) Gyr = pyctrl.feedback(P*K, 1) gain, phase, w = pyctrl.bode(Gyr, pyctrl.logspace(-1,2), plot=False) ax1.plot(w/(2*np.pi), 20*np.log10(gain), label='pyctrl') ax2.plot(w/(2*np.pi), phase*180/np.pi, label='pyctrl') ax2.set_ylim(-190, 10); ax2.set_yticks([-180, -90, 0]) ax1.legend(); ax1.grid(); ax1.set_xscale('log') ax1.set_ylabel('Gain [dB]') ax2.legend(); ax2.grid(); ax2.set_xscale('log') ax2.set_xlabel('[Hz]') ax2.set_ylabel('Phase [deg]') fig.tight_layout()

PD制御
D制御を加えることで、振動を抑えることができる
kp = 2 kd = 0.2
ステップ応答
目標値と現在値の差分(偏差)を演算し、
前回の偏差との差分からD成分を算出する
dt = 0.0001 t_s = [0.0] x_s = [0.0] v_s = [0.0] a_s = [0.0] F_s = [0.0] ref_s = [0.0] pre_err = 0.0 for i in range(20000): ref = target ref_s += [ref] err = ref - x_s[-1] F_s += [ err * kp + (err - pre_err) * kd / dt] a_s += [(- mu * v_s[-1] - M * g * l * x_s[-1] + F_s[-1]) / J] v_s += [v_s[-1] + a_s[-1] * dt] x_s += [x_s[-1] + v_s[-1] * dt] t_s += [t_s[-1] + dt] pre_err = err df = pd.DataFrame() df['in'] = F_s[::100] df['out'] = x_s[::100] df.index = t_s[::100]
fig = plt.figure(figsize=(6, 5)) ax1 = fig.add_subplot(1, 1, 1) ax1.plot(df.index, df['out'], '.-', label='sim') # controlモジュールによるステップ応答と比較 P = pyctrl.tf([0, 1], [J, mu, M *g *l]) K = pyctrl.tf([kd, kp], [0, 1]) Gyr = pyctrl.feedback(P * K, 1) y,t = pyctrl.step(Gyr, np.arange(0, 2, 0.01)) ax1.plot(t, y*target, '-', label='pyctrl') ax1.axhline(target, color="k", linewidth=0.5) ax1.set_xlim(0, 2); ax1.set_ylim(0, 50) ax1.legend(); ax1.grid() ax1.set_ylabel('y'); ax1.set_xlabel('t') fig.tight_layout()
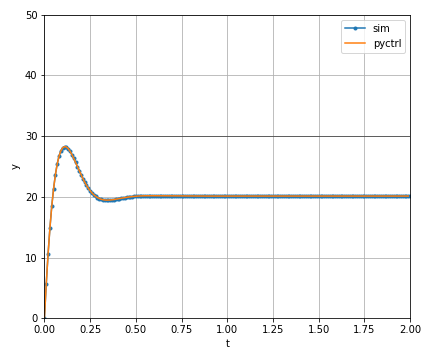
周波数特性
dt = 0.0001 df_list = [] for hz in hz_s: t_s = [0.0] x_s = [0.0] v_s = [0.0] a_s = [0.0] F_s = [0.0] ref_s = [0.0] pre_err = 0.0 for i in range(50000): ref = target * np.sin(2.0 * np.pi * hz * t_s[-1]) ref_s += [ref] err = ref - x_s[-1] F_s += [ err * kp + (err - pre_err) * kd / dt] a_s += [(- mu * v_s[-1] - M * g * l * x_s[-1] + F_s[-1]) / J] v_s += [v_s[-1] + a_s[-1] * dt] x_s += [x_s[-1] + v_s[-1] * dt] t_s += [t_s[-1] + dt] pre_err = err df = pd.DataFrame() df['in'] = ref_s[30000:] df['out'] = x_s[30000:] df.index = t_s[30000:] df_list += [df]
data_s = [] for hz, df in zip(hz_s, df_list): p0 = [target, hz, 0.0] p1, conv = curve_fit(sin_func, np.array(df.index), np.array(df['in']), p0=p0) p0 = [target, hz, 0.0] p2, conv = curve_fit(sin_func, np.array(df.index), np.array(df['out']), p0=p0) param1, param2, freq, gain, phase = calc_f_func(p1, p2) data_s.append([freq, gain, phase]) df_res = pd.DataFrame(data_s) df_res.columns = ['freq', 'gain', 'phase']
fig = plt.figure(figsize=(6, 5)) ax1 = fig.add_subplot(2, 1, 1) ax2 = fig.add_subplot(2, 1, 2) ax1.plot(df_res['freq'], np.log10(df_res['gain'])*20.0, 'o-', label='sim') ax2.plot(df_res['freq'], df_res['phase'], 'o-', label='sim') K = pyctrl.tf([kd, kp], [0, 1]) Gyr = pyctrl.feedback(P*K, 1) gain, phase, w = pyctrl.bode(Gyr, pyctrl.logspace(-1,2), plot=False) ax1.plot(w/(2*np.pi), 20*np.log10(gain), label='pyctrl') ax2.plot(w/(2*np.pi), phase*180/np.pi, label='pyctrl') ax2.set_ylim(-190, 10); ax2.set_yticks([-180, -90, 0]) ax1.legend(); ax1.grid(); ax1.set_xscale('log') ax1.set_ylabel('Gain [dB]') ax2.legend(); ax2.grid(); ax2.set_xscale('log') ax2.set_xlabel('[Hz]') ax2.set_ylabel('Phase [deg]') fig.tight_layout()

D制御で、ピークゲインが抑えられ、振動が小さくなる
PID制御
I制御を加えて、定常偏差を押さえる
kp = 2 kd = 0.1 ki = 10
ステップ応答
偏差を積算し、I成分として使用する
dt = 0.0001 t_s = [0.0] x_s = [0.0] v_s = [0.0] a_s = [0.0] F_s = [0.0] ref_s = [0.0] pre_err = 0.0 integ = 0.0 for i in range(20000): ref = target ref_s += [ref] err = ref - x_s[-1] integ += err F_s += [ err * kp + (err - pre_err) * kd / dt + integ * ki * dt] a_s += [(- mu * v_s[-1] - M * g * l * x_s[-1] + F_s[-1]) / J] v_s += [v_s[-1] + a_s[-1] * dt] x_s += [x_s[-1] + v_s[-1] * dt] t_s += [t_s[-1] + dt] pre_err = err df = pd.DataFrame() df['in'] = F_s[::100] df['out'] = x_s[::100] df.index = t_s[::100]
fig = plt.figure(figsize=(6, 5)) ax1 = fig.add_subplot(1, 1, 1) ax1.plot(df.index, df['out'], '.-', label='sim') # controlモジュールによるステップ応答と比較 P = pyctrl.tf([0, 1], [J, mu, M *g *l]) K = pyctrl.tf([kd, kp, ki], [1, 0]) Gyr = pyctrl.feedback(P * K, 1) y,t = pyctrl.step(Gyr, np.arange(0, 2, 0.01)) ax1.plot(t, y*target, '-', label='pyctrl') ax1.axhline(target, color="k", linewidth=0.5) ax1.set_xlim(0, 2); ax1.set_ylim(0, 50) ax1.legend(); ax1.grid() ax1.set_ylabel('y'); ax1.set_xlabel('t') fig.tight_layout()

周波数特性
dt = 0.0001 df_list = [] for hz in hz_s: t_s = [0.0] x_s = [0.0] v_s = [0.0] a_s = [0.0] F_s = [0.0] ref_s = [0.0] pre_err = 0.0 integ = 0.0 for i in range(50000): ref = target * np.sin(2.0 * np.pi * hz * t_s[-1]) ref_s += [ref] err = ref - x_s[-1] integ += err F_s += [ err * kp + (err - pre_err) * kd / dt + integ * ki * dt] a_s += [(- mu * v_s[-1] - M * g * l * x_s[-1] + F_s[-1]) / J] v_s += [v_s[-1] + a_s[-1] * dt] x_s += [x_s[-1] + v_s[-1] * dt] t_s += [t_s[-1] + dt] pre_err = err df = pd.DataFrame() df['in'] = ref_s[30000:] df['out'] = x_s[30000:] df.index = t_s[30000:] df_list += [df]
data_s = [] for hz, df in zip(hz_s, df_list): p0 = [target, hz, 0.0] p1, conv = curve_fit(sin_func, np.array(df.index), np.array(df['in']), p0=p0) p0 = [target, hz, 0.0] p2, conv = curve_fit(sin_func, np.array(df.index), np.array(df['out']), p0=p0) param1, param2, freq, gain, phase = calc_f_func(p1, p2) data_s.append([freq, gain, phase]) df_res = pd.DataFrame(data_s) df_res.columns = ['freq', 'gain', 'phase']
fig = plt.figure(figsize=(6, 5)) ax1 = fig.add_subplot(2, 1, 1) ax2 = fig.add_subplot(2, 1, 2) ax1.plot(df_res['freq'], np.log10(df_res['gain'])*20.0, 'o-', label='sim') ax2.plot(df_res['freq'], df_res['phase'], 'o-', label='sim') K = pyctrl.tf([kd, kp, ki], [1, 0]) Gyr = pyctrl.feedback(P*K, 1) gain, phase, w = pyctrl.bode(Gyr, pyctrl.logspace(-1,2), plot=False) ax1.plot(w/(2*np.pi), 20*np.log10(gain), label='pyctrl') ax2.plot(w/(2*np.pi), phase*180/np.pi, label='pyctrl') ax2.set_ylim(-190, 10); ax2.set_yticks([-180, -90, 0]) ax1.legend(); ax1.grid(); ax1.set_xscale('log') ax1.set_ylabel('Gain [dB]') ax2.legend(); ax2.grid(); ax2.set_xscale('log') ax2.set_xlabel('[Hz]') ax2.set_ylabel('Phase [deg]') fig.tight_layout()
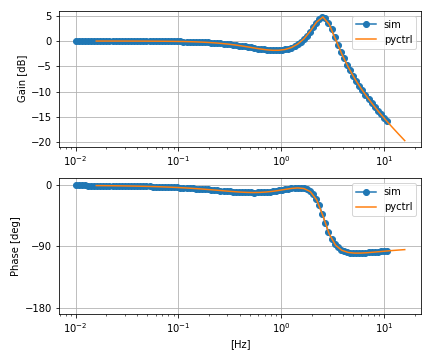
I制御により、低域のゲインが上がり、定常偏差がなくなる
参考文献
この記事は以下の書籍を参考にしましたが、
私の拙い知識で書いておりますので、誤り等ありましたらご指摘ください
